㈠ 立方晶型结构问题

⒈ 如果晶体中最小的重复单元(即晶胞)是立方体，则根据晶胞的组成和结构模型加以想象，可推断晶体组成微粒数目之比及晶胞中组成微粒个数。其计算思路如下：

⑴凡处于立方体顶点位置的微粒(简称“顶点”)，同时为8个晶胞所共用，因此每个“顶点”只有1／8属于该晶胞；

⑵凡处于立方体棱边上的微粒(简称“棱点”)，同时为4个晶胞所共用，因此每个“棱点”只有1／4属于该晶胞；

⑶凡处于立方体面上的微粒(简称“面心”)，同时为2个晶胞共用，因此每个“面心”的1／2属于该晶胞；

⑷凡处于立方体内部的微粒(简称“体心”)，完全属于该晶胞。

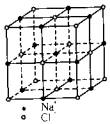
⒉ NaCl 晶体

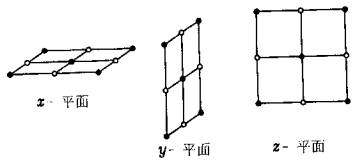
由NaCl晶胞结构示意图可知，一个晶胞中：Na^＋的个数=1(体心)＋12×(1／4)(棱点)=4(个)，Cl^－的个数=8×(1／8)(顶点)＋6×(1／2)(面心)=4(个)

居于立方体中心的Na^＋，实际上共有3个平面通过它。如将这3个平面分别称为X^－平面、Y^－平面、Z^－平面，画出来即如图所示。可以清楚地看出，在通过中心Na^＋的3个平面内，每个平面都有4个Na^＋居于平面的4个角上(也即4个顶点上)，这4个Na^＋与中心Na^＋距离最近且距离相等。因此NaCl晶体中每个Na^＋周围与它最接近且距离相等的Na^＋共12个。同理Cl^－也可以得出同样结论。

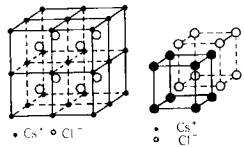
⒊ CsCl晶体

由CsCl晶体结构示意图可知：1个Cs^＋同时吸引着8个Cl^－，1个Cl^－同时吸引着8个Cs^＋；与1个Cs^＋最近且距离相等的Cs^＋有6个，与1个Cl^－最近且距离相等的Cl^－也有6个。

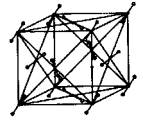
⒋ 干冰晶体

根据干冰晶体微小立方体结构示意图：

在每个CO₂周围等距离且相距最近的CO₂共有12个。

在每个小立方体中平均分摊到的CO₂分子数=8×(1／8)(顶点)＋6×(1／2)(面心)=4(个)

㈡ 笼状结构或无限网状结构问题

对于笼状结构或无限网状结构中的基本单元的有关问题解答，关键是要弄清这一基本结构单元中的一个点或一条边为多少个基本单元所共有，如果为n个单元所共有，则这一点或这一条边对于一个基本单元的“贡献”就为1/n。

⒈ 金刚石

在金刚石晶体中，碳原子构成的最小环为非平面六元环(与环己烷碳环相似)，键角为109°28′，每个碳原子与相邻4个碳原子构成“实心”正四面体，其n(C)：n(C-C)=1∶(4×1/2)=1∶2。每个碳原子被多少个六元环共用呢？以1号碳为例，相邻两条C—C键可构成2个六元环，根据数学上的排列组合原理，它共有C²₄种这种相邻，故被2C²₄=12个六元环共用。同理，每条C—C键被2C¹₃=6个六元环共用。

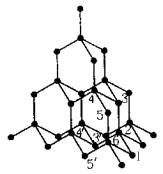
⒉ 石墨

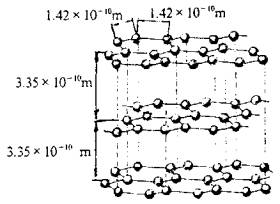
在石墨晶体中，碳原子构成的最小环为平面型六元环(与苯环相似)，键角为120°，每个碳原子与相邻3个碳原子构成“实心”正三角形。其n(C)：n(C-C)=1∶(3×1／2)=2∶3。每个碳原子被3个六元环共用，每条C—C键被2个六元环共用。

⒊ C₆₀

C₆₀分子中含有12个五边形、20个六边形，存在以下等量关系：

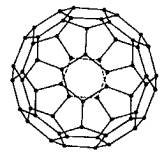
⑴ 欧拉定理：顶点数＋面数棱边数=2

⑵ 考虑面对棱的分割：棱边数=五边形数×5/2＋六边形数×6/2

⑶ 考虑点对棱的分割：棱边数=顶点数×3/2

⑷ 考虑面对点的分割：顶点数=五边形数×5/3＋六边形数×6/3

⑸ 考虑总价电子数：顶点数×4=单键数×2＋双键数×4

⑹ 考虑每个C只能形成两条C-C及一条C=C：单键数=双键数×2

⒋ SiO₂晶体

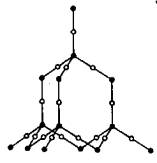
可以这样去理解SiO₂的结构，即在晶体硅(结构同金刚石)中的Si—Si键间插入1个O原子。晶体中存在SiO₄四面体及OSiO折线，∠OSiO=109°28′，∠SiOSi＝104.5°(与HOH中键角相似)。晶体中最小环为十二元环，由6个Si和6个O构成。每个Si被2C²₄=12个十二元环共用，每个O被2C¹₃=6个十二元环共用。